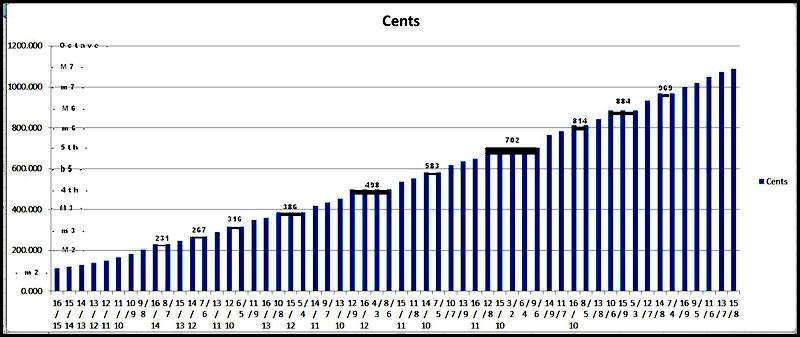
This contains all the ratios within upper limit 16;
sorted on the cents value and put them in graph mode.
When you look at the graph,
the ratios are along the bottom axis and
the number of cents display vertically.
Some ratios have the same cents value (3/2 = 6/4 = 9/6 = ...)
and therefore appear more than once.
These would have constructive resonance and
be more prominent, stronger, or louder harmonics:
the harmonic sweet spots.

The fifth (at 702 cents) having 5 constructive ratios
is the obvious most prominent sweet spot
in the spectrum of an octave.
The forth (at 498 cents) is the next most promenent
with 4 constructive ratios within the 16 upper limit.
The slightly flatted major third (at 386 cents)
and the slightly flatted minor sixth (at 884 cents)
are the next most resonaant harmonics with 3.
Then we have 3 notes between the M2 and the M3
(at 231, 267, and 316 cents) as well as a
slightly flatted (b5) flatted fifth (at 583 cents) and a very flatted minor seventh (at 969 cents).
I am a picture person and
having a visual to work off of helps me to refine my sound.
Playing shakuhachi and Anasazi, simple bamboo vertical flutes,
there's no setting of notes to hit,
but any note can be played by changing angle and/or embouchure.

I study Shakuhachi Honkyoku which proceeded western music
but has been shoe horned into the equal temperament box
(12 notes per octave), but which does not fit well.
I find 12 EDO Equal Temperament very limiting:
12 notes per octave has nothing to do with the true nature of sound.
Would an artist limit them self to twelve colors of paints
instead of the whole rainbow of colors?
Equal Temperament is an experiment in compromise
created for tuning pianos in the classical era.
Much great music has been created in this system
and jazz would be impossible without it,
however I am drawn to natural and healing music,
which is Just Intonation (pure temperament).

For a high resolution image (opens in a new tab):
JI_Upper_Limit_16.jpg

---